Effective Rates Can Be Seen in the Compounding Table for One Dollar.

What is the Effective Annual Interest Charge per unit?

The Constructive Annual Interest Charge per unit (EAR) is the involvement rate that is adjusted for compounding Compound Growth Rate The compound growth rate is a measure used specifically in business and investing contexts, that indicates the growth rate over multiple fourth dimension periods. It is a measure of the constant growth of a data series. The biggest reward of the compound growth rate is that the metric takes into consideration the compounding result. over a given period. But put, the constructive annual interest charge per unit is the rate of interest Involvement Expense Interest expense arises out of a company that finances through debt or capital leases. Involvement is plant in the income statement, but can likewise that an investor can earn (or pay) in a yr subsequently taking into consideration compounding.

EAR can be used to evaluate interest payable on a loan or whatsoever debt or to appraise earnings from an investment, such as a guaranteed investment document (GIC) or savings account.

The effective annual interest charge per unit is also known as the effective interest rate (EIR), annual equivalent charge per unit (AER), or effective rate. Compare it to the Almanac Percentage Rate (April) Almanac Per centum Rate (Apr) The Annual Percentage Charge per unit (Apr) is the yearly charge per unit of interest that an individual must pay on a loan, or that they receive on a deposit account. Ultimately, April is a simple percentage term used to express the numerical corporeality paid by an individual or entity yearly for the privilege of borrowing money. which is based on simple interest Unproblematic Interest Simple interest formula, definition and instance. Simple interest is a calculation of interest that doesn't take into business relationship the event of compounding.  In many cases, involvement compounds with each designated period of a loan, but in the case of simple interest, it does not.  The calculation of simple interest is equal to the principal amount multiplied by the interest rate, multiplied by the number of periods. .

The EAR formula is given below:

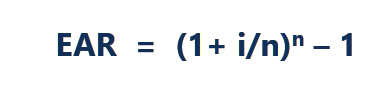
Where:

• i = Stated annual interest charge per unit
• northward = Number of compounding periods

Constructive Annual Rate Based on Compounding

The table below shows the difference in the effective almanac rate when the compounding periods modify.

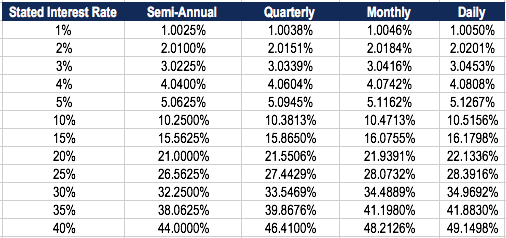
Tabular array: CFI's Fixed Income Fundamentals Course

For instance, the EAR of a 1% Stated Interest Charge per unit compounded quarterly is ane.0038%.

Importance of Effective Annual Rate

The effective annual interest charge per unit is an of import tool that allows the evaluation of the true return on an investment or truthful involvement rate on a loan.

The stated almanac interest rate and the effective involvement charge per unit can exist significantly unlike, due to compounding. The effective involvement rate is important in figuring out the best loan or determining which investment offers the highest charge per unit of return. Internal Rate of Return (IRR) The Internal Rate of Render (IRR) is the discount rate that makes the net present value (NPV) of a project zero. In other words, information technology is the expected compound almanac charge per unit of render that volition be earned on a project or investment.

In the case of compounding, the EAR is always college than the stated almanac involvement rate.

EAR Example

For example, assume the bank offers your eolith of $10,000 a 12% stated interest rate compounded monthly. The table beneath demonstrates the concept of the effective annual interest rate:

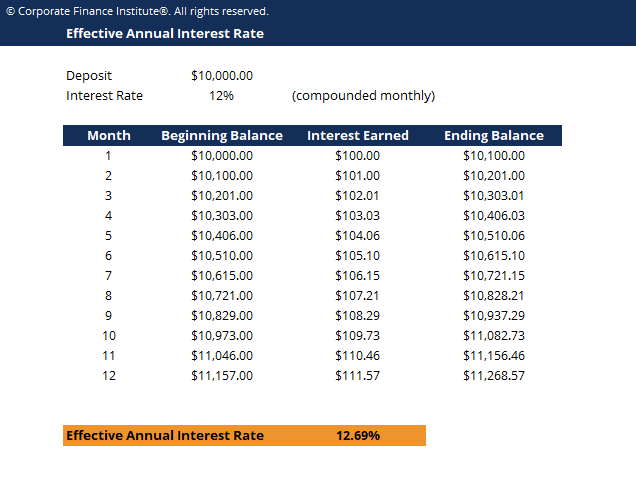Tabular array: CFI's Stock-still Income Fundamentals Form

Month 1 Interest: Outset Rest ($ten,000) 10 Interest Rate (12%/12 = 1%) = $100

Month 2 Interest: Beginning Rest ($10,100) x Involvement Charge per unit (12%/12 = 1%) = $101

The change, in percentage, from the starting time balance ($ten,000) to the ending balance ($xi,268) is ($11,268 – $10,000)/$10,000 = .12683 or 12.683%, which is the effective annual interest charge per unit. Even though the bank offered a 12% stated involvement rate, your money grew by 12.683% due to monthly compounding.

The effective almanac involvement rate allows you to determine the true render on investment (ROI) ROI Formula (Return on Investment) Return on investment (ROI) is a financial ratio used to summate the benefit an investor will receive in relation to their investment cost. It is most commonly measured every bit internet income divided past the original majuscule cost of the investment. The higher the ratio, the greater the benefit earned. .

Download the Free Template

Enter your name and email in the form below and download the free template shown in a higher place now!

Effective Annual Interest Rate Calculator

Download the gratis Excel template now to accelerate your finance knowledge!

How to Calculate the Effective Involvement Rate?

To calculate the constructive involvement rate using the EAR formula, follow these steps:

1. Determine the stated involvement rate

The stated interest rate (as well called the annual per centum rate or nominal charge per unit) is usually found in the headlines of the loan or deposit agreement. Example: "Annual charge per unit 36%, involvement charged monthly."

2. Determine the number of compounding periods

The compounding periods are typically monthly or quarterly. The compounding periods may be 12 (12 months in a year) and iv for quarterly (4 quarters in a year).

For your reference:

• Monthly = 12 compounding periods
• Quarterly = 4 compounding periods
• Bi-Weekly = 26 compounding periods
• Weekly = 52 compounding periods
• Daily = 365 compounding periods

three. Utilise the EAR Formula: EAR = (ane+ i/n)^north – i

Where:

• i = Stated interest rate
• n = Compounding periods

Example

To calculate the effective annual interest rate of a credit card with an annual rate of 36% and interest charged monthly:

1. Stated interest rate: 36%

two. Number of compounding periods: 12

Therefore, EAR = (1+0.36/12)^12 – 1 = 0.4257 or 42.57%.

Why Don't Banks Use the Effective Annual Involvement Rate?

When banks are charging interest, the stated interest rate is used instead of the effective annual interest rate. This is done to make consumers believe that they are paying a lower interest rate.

For example, for a loan at a stated interest rate of 30%, compounded monthly, the effective almanac interest rate would exist 34.48%. Banks will typically advertise the stated interest rate of thirty% rather than the effective interest rate of 34.48%.

When banks are paying interest on your deposit business relationship, the EAR is advertised to look more attractive than the stated interest charge per unit.

For example, for a eolith at a stated rate of 10% compounded monthly, the constructive almanac interest rate would be 10.47%. Banks volition advertise the effective annual interest charge per unit of 10.47% rather than the stated interest charge per unit of 10%.

Substantially, they testify whichever rate appears more than favorable.

Related Reading

Thank yous for reading CFI's guide on Effective Annual Involvement Rate. To continue developing your career every bit a financial professional, cheque out the following additional CFI resources:

• Expected Return Expected Return The expected return on an investment is the expected value of the probability distribution of possible returns information technology can provide to investors. The return on the investment is an unknown variable that has different values associated with different probabilities.
• Basis Points Ground Points (BPS) Basis Points (BPS) are the unremarkably used metric to gauge changes in involvement rates. A basis bespeak is 1 hundredth of 1 percent.
• Capital letter Gains Yield Capital letter Gains Yield Majuscule gains yield (CGY) is the price appreciation on an investment or a security expressed equally a percent. Considering the calculation of Majuscule Gain Yield involves the market price of a security over time, it can exist used to analyze the fluctuation in the market cost of a security. Encounter calculation and example
• Weighted Boilerplate Toll of Capital (WACC) WACC WACC is a firm's Weighted Average Price of Upper-case letter and represents its blended price of upper-case letter including disinterestedness and debt.

colethereave.blogspot.com

Source: https://corporatefinanceinstitute.com/resources/knowledge/finance/effective-annual-interest-rate-ear/